https://doi.org/10.1140/epjc/s10052-024-13291-7
Regular Article - Theoretical Physics
Criticality of the O(N) universality via global solutions to nonperturbative fixed-point equations
School of Physics, Dalian University of Technology, 116024, Dalian, People’s Republic of China
Received:
10
August
2023
Accepted:
23
August
2024
Published online:
5
September
2024
Fixed-point equations in the functional renormalization group approach are integrated from large to vanishing field, where an asymptotic potential in the limit of large field is implemented as initial conditions. This approach allows us to obtain a global fixed-point potential with high numerical accuracy, that incorporates the correct asymptotic behavior in the limit of large field. Our calculated global potential is in good agreement with the Taylor expansion in the region of small field, and it also coincides with the Laurent expansion in the regime of large field. Laurent expansion of the potential in the limit of large field for general case, that the spatial dimension d is a continuous variable in the range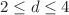 
, is obtained. Eigenfunctions and eigenvalues of perturbations near the Wilson–Fisher fixed point are computed with the method of eigenperturbations. Critical exponents for different values of d and N of the O(N) universality class are calculated.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
