Study of complexity factor and stability of dynamical systems in gravity

M. Zeeshan Gul; W. Ahmad; M. M. M. Nasir; Faisal Javed; Orhan Donmez; Bander Almutairi

doi:10.1140/epjc/s10052-025-14163-4

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2025) 85: 595
https://doi.org/10.1140/epjc/s10052-025-14163-4

Regular Article - Theoretical Physics

Study of complexity factor and stability of dynamical systems in $f (G)$ $f(\mathcal {G})$ gravity

M. Zeeshan Gul¹^,2^,3, W. Ahmad², M. M. M. Nasir⁴^a, Faisal Javed⁶^b, Orhan Donmez⁵ and Bander Almutairi⁷

¹ College of Transportation, Tongji University, 201804, Shanghai, China
² Research Center of Astrophysics and Cosmology, Khazar University, 41 Mehseti Street, AZ1096, Baku, Azerbaijan
³ Department of Mathematics and Statistics, The University of Lahore, 1-KM Defence Road, 54000, Lahore, Pakistan
⁴ Hajvery University Gulberg 3, Lahore, Pakistan
⁵ College of Engineering and Technology, American University of the Middle East, 54200, Egaila, Kuwait
⁶ Department of Physics, Zhejiang Normal University, 321004, Jinhua, People’s Republic of China
⁷ Department of Mathematics, College of Science, King Saud University, P.O. Box 2455, 11451, Riyadh, Saudi Arabia

^a muddassarnasir6666@gmail.com
^b faisaljaved.math@gmail.com

Received: 10 February 2025
Accepted: 6 April 2025
Published online: 29 May 2025

Abstract

In this paper, we evaluate the complexity of the non static cylindrical geometry with anisotropic matter configuration in the framework of modified Gauss–Bonnet theory. In this perspective, we calculate modified field equations, the C energy formula and the mass function that help to understand the astrophysical structures in this modified gravity. Furthermore, we use the Weyl tensor and obtain different structure scalars by orthogonally splitting the Riemann tensor. One of these scalars, 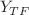$Y_{TF}$ $Y_{TF}$ is referred to as the complexity factor. This parameter measures the system’s complexity due to non-uniform energy density and non-isotropic pressure. We select the identical complexity factor for the structure as used in the non-static scenario, while considering the analogous criterion for the most elementary pattern of development. This technique involves formulating structural scalars that illustrate the fundamental features of the system. A fluid distribution that satisfies the vanishing complexity requirement and evolves homologously is characterized as isotropic, geodesic, homogeneous, and shear-free. In the dissipative scenario, the fluid remains geodesic while exhibiting shear, resulting in an extensive array of solutions.

© The Author(s) 2025

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.