https://doi.org/10.1140/epjc/s10052-025-14067-3
Regular Article - Theoretical Physics
Proton spin in double-logarithmic approximation
Ioffe Institute, 194021, St. Petersburg, Russia
Received:
19
December
2024
Accepted:
10
March
2025
Published online:
29
March
2025
Proton is a composite particle, so its spin 
is made from the spins of the partons which the proton consists of the discrepancy between 
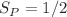and the experimentally detected sum of the parton spins was named Proton Spin Puzzle. Solution to this problem includes formulae for the parton helicities valid in the whole range of x. There are approaches in the literature for calculating the helicities. As a theoretical basis they apply evolution equations of different types. Despite these equations are constructed for operating in widely different regions of x and account for different contributions, all of them equally well suited for solving the proton spin problem. Our explanation of this situation is that the main impact on values of the parton spin contributions should be brought not by the evolution equations themselves but by phenomenological fits for initial parton distributions. We suggest a more theoretically grounded approach to description of the parton helicities and apply it to solving the proton spin problem. It combines the total resummation of double logarithms (DL), accounting for the running 
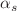effects and DGLAP formulae, leading to expressions for the helicities valid at arbitrary x. As a consequence, the set of involved phenomenological parameters in our approach is minimal and its influence on the helicity behaviour is weak. We apply our approach to solve the proton spin problem in a straightforward way and make an estimate, demonstrating that the RHIC data complemented by the DL contributions from the regions of x beyond the RHIC scope are well compatible with the value 
.
© The Author(s) 2025
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
