https://doi.org/10.1140/epjc/s10052-024-13664-y
Regular Article - Theoretical Physics
Regular black holes from Kiselev anisotropic fluid
Departamento de Física, CFM-Universidade Federal de Santa Catarina, C.P. 476, CEP 88.040-900, Florianópolis, SC, Brazil
Received:
4
October
2024
Accepted:
27
November
2024
Published online:
26
December
2024
In this paper, we investigate a generalization of Kiselev black holes by introducing a varying equation-of-state parameter for the anisotropic fluid surrounding the black hole. We extend this model by allowing w in the expression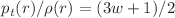 
to vary as a function of the radial coordinate, and derive new solutions to the Einstein field equations for this configuration. In particular, we study solutions that describe regular black holes. By choosing specific forms of w(r), we obtain regular black hole solutions, and show that the matter surrounding the black hole can satisfy the weak and strong energy conditions under certain values of parameters analyzed. Due to the generality of this treatment, other categories of black holes can be obtained with particular choices of the equation-of-state parameter. Our analysis confirms that the curvature invariants associated with the regular black holes remain finite at the origin, indicating the absence of singularities. We also explore the physical properties of the matter associated with these solutions. Due to its versatility, we suggest the possibility of using this approach as a tool to construct new physical solutions associated with regular black holes or other geometries of interest.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
