https://doi.org/10.1140/epjc/s10052-024-13309-0
Regular Article - Theoretical Physics
Planar decomposition of the HOMFLY polynomial for bipartite knots and links
1
Moscow Institute of Physics and Technology, 141700, Dolgoprudny, Russia
2
Institute for Information Transmission Problems, 127051, Moscow, Russia
3
NRC “Kurchatov Institute”, 123182, Moscow, Russia
4
Institute for Theoretical and Experimental Physics, 117218, Moscow, Russia
Received:
17
July
2024
Accepted:
26
August
2024
Published online:
30
September
2024
The theory of the Kauffman bracket, which describes the Jones polynomial as a sum over closed circles formed by the planar resolution of vertices in a knot diagram, can be straightforwardly lifted from 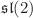 to
to 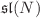 at arbitrary N – but for a special class of bipartite diagrams made entirely from the antiparallel lock tangle. Many amusing and important knots and links can be described in this way, from twist and double braid knots to the celebrated Kanenobu knots for even parameters – and for all of them the entire HOMFLY polynomials possess planar decomposition. This provides an approach to evaluation of HOMFLY polynomials, which is complementary to the arborescent calculus, and this opens a new direction to homological techniques, parallel to Khovanov–Rozansky generalizations of the Kauffman calculus. Moreover, this planar calculus is also applicable to other symmetric representations beyond the fundamental one, and to links which are not fully bipartite what is illustrated by examples of Kanenobu-like links.
at arbitrary N – but for a special class of bipartite diagrams made entirely from the antiparallel lock tangle. Many amusing and important knots and links can be described in this way, from twist and double braid knots to the celebrated Kanenobu knots for even parameters – and for all of them the entire HOMFLY polynomials possess planar decomposition. This provides an approach to evaluation of HOMFLY polynomials, which is complementary to the arborescent calculus, and this opens a new direction to homological techniques, parallel to Khovanov–Rozansky generalizations of the Kauffman calculus. Moreover, this planar calculus is also applicable to other symmetric representations beyond the fundamental one, and to links which are not fully bipartite what is illustrated by examples of Kanenobu-like links.
© The Author(s) 2024
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.




