https://doi.org/10.1140/epjc/s10052-022-10969-8
Regular Article - Theoretical Physics
Defect and degree of the Alexander polynomial
1
Moscow Institute of Physics and Technology, 141701, Dolgoprudny, Russia
2
Institute for Theoretical and Experimental Physics, 117218, Moscow, Russia
3
Institute for Information Transmission Problems, 127051, Moscow, Russia
4
NRC “Kurchatov Institute”, 123182, Moscow, Russia
Received:
6
August
2022
Accepted:
28
October
2022
Published online:
14
November
2022
Defect characterizes the depth of factorization of terms in differential (cyclotomic) expansions of knot polynomials, i.e. of the non-perturbative Wilson averages in the Chern-Simons theory. We prove the conjecture that the defect can be alternatively described as the degree in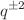 
of the fundamental Alexander polynomial, which formally corresponds to the case of no colors. We also pose a question if these Alexander polynomials can be arbitrary integer polynomials of a given degree. A first attempt to answer the latter question is a preliminary analysis of antiparallel descendants of the 2-strand torus knots, which provide a nice set of examples for all values of the defect. The answer turns out to be positive in the case of defect zero knots, what can be observed already in the case of twist knots. This proved conjecture also allows us to provide a complete set of C-polynomials for the symmetrically colored Alexander polynomials for defect zero. In this case, we achieve a complete separation of representation and knot variables.
© The Author(s) 2022
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
