Simple representations of BPS algebras: the case of

Dmitry Galakhov; Alexei Morozov; Nikita Tselousov

doi:10.1140/epjc/s10052-024-12952-x

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2024) 84: 604
https://doi.org/10.1140/epjc/s10052-024-12952-x

Regular Article - Theoretical Physics

Simple representations of BPS algebras: the case of $Y ({\hat{gl}}_{2})$ $Y(\widehat{\mathfrak {gl}}_2)$

Dmitry Galakhov²^,3^,4, Alexei Morozov¹^,2^,3^,4 and Nikita Tselousov¹^,2^,4^c

¹ MIPT, 141701, Dolgoprudny, Russia
² NRC “Kurchatov Institute”, 123182, Moscow, Russia
³ IITP RAS, 127051, Moscow, Russia
⁴ ITEP, Moscow, Russia

^c tselousov.ns@phystech.edu

Received: 3 May 2024
Accepted: 23 May 2024
Published online: 10 June 2024

Abstract

BPS algebras are the symmetries of a wide class of brane-inspired models. They are closely related to Yangians – the peculiar and somewhat sophisticated limit of DIM algebras. Still they possess some simple and explicit representations. We explain here that for $Y ({\hat{gl}}_{r})$ $Y(\widehat{\mathfrak {gl}}_r)$ these representations are related to Uglov polynomials, whose families are also labeled by natural r. 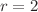They arise in the limit $ħ ⟶ 0$ $\hbar {\longrightarrow } 0$ from Macdonald polynomials, and generalize the well-known Jack polynomials ( $β$ $\beta$ -deformation of Schur functions), associated with $r = 1 .$ $$r=1.$$ For $r = 2$ $$r=2$$ they approximate Macdonald polynomials with the accuracy $O (ħ^{2}),$ $O(\hbar ^2),$ so that they are eigenfunctions of two immediately available commuting operators, arising from the $ħ$ $\hbar$ -expansion of the first Macdonald Hamiltonian. 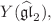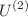These operators have a clear structure, which is easily generalizable, – what provides a technically simple way to build an explicit representation of Yangian $Y ({\hat{gl}}_{2}),$ $Y(\widehat{\mathfrak {gl}}_2),$ where $U^{(2)}$ $U^{(2)}$ are associated with the states $| λ ⟩,$ $|\lambda {\rangle },$ parametrized by chess-colored Young diagrams. 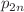An interesting feature of this representation is that the odd time-variables $p_{2 n + 1}$ $p_{2n+1}$ can be expressed through mutually commuting operators from Yangian, however even time-variables $p_{2 n}$ $p_{2n}$ are inexpressible. Implications to higher r become now straightforward, yet we describe them only in a sketchy way.

© The Author(s) 2024

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.