https://doi.org/10.1140/epjc/s10052-024-12878-4
Regular Article - Theoretical Physics
Phase-space analysis in non-minimal symmetric-teleparallel dark energy
1
Università di Camerino, Via Madonna delle Carceri, 62032, Camerino, Italy
2
INAF-Osservatorio Astronomico di Brera, Milan, Italy
3
SUNY Polytechnic Institute, 13502, Utica, NY, USA
4
Istituto Nazionale di Fisica Nucleare (INFN), Sezione di Perugia, 06123, Perugia, Italy
5
Al-Farabi Kazakh National University, Al-Farabi av. 71, 050040, Almaty, Kazakhstan
Received:
23
January
2024
Accepted:
3
May
2024
Published online:
24
May
2024
We modify the symmetric-teleparallel dark energy through the addition of a further Yukawa-like term, in which the non-metricity scalar, Q, is non-minimally coupled to a scalar field Lagrangian where the phion acts as quintessence, describing dark energy. We investigate regions of stability and find late-time attractors. To do so, we conduct a stability analysis for different types of physical potentials describing dark energy, namely the power-law, inverse power-law, and exponential potentials. Within these choices, we furthermore single out particular limiting cases, such as the constant, linear and inverse potentials. For all the considered scenarios, regions of stability are calculated in terms of the signs of the coupling constant and the exponent, revealing a clear degeneracy among coefficients necessary to ensure stability. We find that a generic power-law potential with 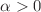 is not suitable as a non-minimal quintessence potential and we put severe limits on the use of inverse potential, as well. In addition, the equations of state of each potential have been also computed. We find the constant potential seems to be favored than other treatments, since the critical point appears independent of the non-minimal coupling.
is not suitable as a non-minimal quintessence potential and we put severe limits on the use of inverse potential, as well. In addition, the equations of state of each potential have been also computed. We find the constant potential seems to be favored than other treatments, since the critical point appears independent of the non-minimal coupling.
© The Author(s) 2024
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.




