https://doi.org/10.1140/epjc/s10052-024-13440-y
Regular Article
Geometric and topological corrections to Schwarzschild black hole
1
INAF-Osservatorio Astronomico di Roma, Via Frascati 33, 00040, Monte Porzio Catone, Italy
2
Istituto Nazionale di Fisica Nucleare (INFN), Sezione di Napoli, Via Cinthia 21, 80126, Naples, Italy
3
Scuola Superiore Meridionale, Largo San Marcellino 10, 80138, Naples, Italy
4
University of Camerino, Via Madonna delle Carceri, 62032, Camerino, Italy
5
Department of Mathematics and Physics, SUNY Polytechnic Institute, 13502, Utica, NY, USA
6
INAF-Osservatorio Astronomico di Brera, Milan, Italy
7
Istituto Nazionale di Fisica Nucleare (INFN), Sezione di Perugia, 06123, Perugia, Italy
8
Al-Farabi Kazakh National University, 050040, Almaty, Kazakhstan
Received:
27
April
2024
Accepted:
29
September
2024
Published online:
15
October
2024
In this paper, we compute departures in the black hole thermodynamics induced by either geometric or topological corrections to general relativity. Specifically, we analyze the spherically symmetric spacetime solutions of two modified gravity scenarios with Lagrangians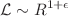 
and 
, where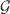 
is the Euler density in four dimensions, while 
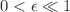measures the perturbation around the Hilbert–Einstein action. Accordingly, we find the expressions of the Bekenstein–Hawking entropy by the Penrose formula, and the black hole temperature and horizon of the obtained solutions. We then investigate the heat capacities in terms of the free parameters of the theories under study. In doing so, we show that healing the problem of negative heat capacities can be possible under particular choices of the free constants, albeit with limitations on the masses allowed for the black hole solutions.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
