https://doi.org/10.1140/epjc/s10052-023-11909-w
Regular Article - Theoretical Physics
Planck length in classical and quantum Hamiltonian formulations of general relativity
Research Center for Theoretical Physics and Astrophysics, Institute of Physics, Silesian University in Opava, Bezručovo nám.13, 74601, Opava, Czech Republic
a
claudiocremaschini@gmail.com
Received:
2
June
2023
Accepted:
6
August
2023
Published online:
16
August
2023
The physical meaning of the Planck length (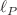
) is investigated in the framework of the unconstrained synchronous variational formulation of classical general relativity (GR). This theoretical setting permits the establishment of manifestly-covariant Lagrangian and Hamiltonian theories for the Einstein field equations of the continuum gravitational field. It is shown that such a formulation is distinguished by the existence of a novel variational contribution expressed by an infinite series summation of suitable 4-scalar terms in which the coupling coefficients are even powers of the Planck length. However, the requirement of realization of a classical GR Hamiltonian theory places stringent constraints on the admissible Planck-length power terms to be retained. In fact, excluding the trivial gauge constant, it is proved that only the 
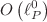contribution of the series is ultimately permitted, namely the unique one which is independent of 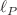. Therefore, the Planck length is effectively not allowed to appear at the classical level for consistency with the Hamiltonian principle. This places important consequences on the mathematical establishment of the corresponding canonical quantum gravity theory, which is then found to be correct through 
. Additional implications concern the physical significance of related quantum momenta and their meaning in the semi-classical limit, as well as the role of the Planck length in the same quantum-gravity realm.
© The Author(s) 2023
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
