https://doi.org/10.1140/epjc/s10052-017-4854-1
Regular Article - Theoretical Physics
Hamiltonian approach to GR – Part 1: covariant theory of classical gravity
1
Faculty of Philosophy and Science, Institute of Physics and Research Center for Theoretical Physics and Astrophysics, Silesian University in Opava, Bezručovo nám.13, 74601, Opava, Czech Republic
2
Department of Mathematics and Geosciences, University of Trieste, Via Valerio 12, 34127, Trieste, Italy
3
Faculty of Philosophy and Science, Institute of Physics, Silesian University in Opava, Bezručovo nám.13, 74601, Opava, Czech Republic
* e-mail: claudiocremaschini@gmail.com
Received:
6
January
2017
Accepted:
21
April
2017
Published online:
19
May
2017
A challenging issue in General Relativity concerns the determination of the manifestly covariant continuum Hamiltonian structure underlying the Einstein field equations and the related formulation of the corresponding covariant Hamilton–Jacobi theory. The task is achieved by adopting a synchronous variational principle requiring distinction between the prescribed deterministic metric tensor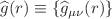 
solution of the Einstein field equations which determines the geometry of the background space-time and suitable variational fields 
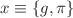obeying an appropriate set of continuum Hamilton equations, referred to here as GR-Hamilton equations. It is shown that a prerequisite for reaching such a goal is that of casting the same equations in evolutionary form by means of a Lagrangian parametrization for a suitably reduced canonical state. As a result, the corresponding Hamilton–Jacobi theory is established in manifestly covariant form. Physical implications of the theory are discussed. These include the investigation of the structural stability of the GR-Hamilton equations with respect to vacuum solutions of the Einstein equations, assuming that wave-like perturbations are governed by the canonical evolution equations.
© The Author(s), 2017
