https://doi.org/10.1140/epjc/s10052-022-10851-7
Regular Article - Theoretical Physics
Differential expansion for antiparallel triple pretzels: the way the factorization is deformed
1
MIPT, 141701, Dolgoprudny, Russia
2
NRC “Kurchatov Institute”, 123182, Moscow, Russia
3
IITP RAS, 127051, Moscow, Russia
4
ITEP, Moscow, Russia
Received:
26
May
2022
Accepted:
26
September
2022
Published online:
14
October
2022
For a peculiar family of double braid knots there is a remarkable factorization formula for the coefficients of the differential (cyclotomic) expansion (DE), which nowadays is widely used to construct the exclusive Racah matrices S and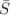 
in arbitrary representations. The origins of the factorization remain obscure and the special role of double braids remains a mystery. In an attempt to broaden the perspective, we extend the family of double braids to antiparallel triple pretzels, which are obtained by the defect-preserving deformation from the trefoil and all have defect zero. It turns out that factorization of DE coefficients is violated quite strongly, still remains described by an elegant formula, at least for all symmetric representations.
© The Author(s) 2022
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
