Eur. Phys. J. C (2022) 82: 696
https://doi.org/10.1140/epjc/s10052-022-10664-8

Regular Article - Theoretical Physics

Shadows and thin accretion disk images of the $\gamma$-metric

¹ Department of Physics, Indian Institute of Technology, 208016, Kanpur, India
² Department of Science and Humanities, Maynaguri Govt. Polytechnic, 735302, Jalpaiguri, India

^d tapo@iitk.ac.in

Received: 7 March 2022
Accepted: 23 July 2022
Published online: 10 August 2022

Abstract

The $\gamma$-metric is a static, axially-symmetric singular solution of the vacuum Einstein’s equations without an event horizon. This is a two-parameter family of solutions, generic values of one of which (called $\gamma$) measure the deviation from spherical symmetry. We show that this can serve as a black hole mimicker, consistent with current observations. To this end, we first study the shadow cast by this geometry, in order to constrain the $\gamma$-metric from observations. 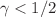We find that for $\gamma <1/2$, there are, in principle, no shadows cast. On the other hand, shadows cast for all values of 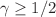$\gamma \ge 1/2$ are consistent with observations of M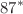${87}^{\ast }$ by the Event Horizon Telescope. We also study images of thin accretion disks in the $\gamma$-metric background. In situations where the $\gamma$-metric possesses light rings, these qualitatively mimic Schwarzschild black holes with the same ADM mass, while in the absence of such rings, they are drastically different from the black hole case.