https://doi.org/10.1140/epjc/s10052-021-09248-9
Regular Article - Theoretical Physics
Duality in elliptic Ruijsenaars system and elliptic symmetric functions
1
Lebedev Physics Institute, 119991, Moscow, Russia
2
ITEP, 117218, Moscow, Russia
3
Institute for Information Transmission Problems, 127994, Moscow, Russia
4
MIPT, 141701, Dolgoprudny, Russia
5
SISSA, Trieste, Italy
6
INFN, Sezione di Trieste, IGAP, Trieste, Italy
7
ITMP, Moscow, Russia
a mironov@lpi.ru, mironov@itep.ru
Received:
7
March
2021
Accepted:
16
May
2021
Published online:
26
May
2021
We demonstrate that the symmetric elliptic polynomials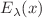 
originally discovered in the study of generalized Noumi–Shiraishi functions are eigenfunctions of the elliptic Ruijsenaars–Schneider (eRS) Hamiltonians that act on the mother function variable 
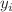(substitute of the Young-diagram variable 
). This means they are eigenfunctions of the dual eRS system. At the same time, their orthogonal complements in the Schur scalar product, 
are eigenfunctions of the elliptic reduction of the Koroteev–Shakirov (KS) Hamiltonians. This means that these latter are related to the dual eRS Hamiltonians by a somewhat mysterious orthogonality transformation, which is well defined only on the full space of time variables, while the coordinates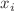 
appear only after the Miwa transform. This observation explains the difficulties with getting the apparently self-dual Hamiltonians from the double elliptic version of the KS Hamiltonians.
© The Author(s) 2021
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
