https://doi.org/10.1140/epjc/s10052-021-08963-7
Regular Article – Theoretical Physics
Embedding cosmology and gravity
1
Department of Physics, State University of New York (SUNY) at Buffalo, 14260, Buffalo, NY, USA
2
Department of Mathematics, State University of New York (SUNY) at Buffalo, 14260, Buffalo, NY, USA
Received:
25
September
2020
Accepted:
8
February
2021
Published online:
13
February
2021
I start with a scenario where the universe is an abstract space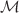 
having d dimensions. There is a two dimensional surface embedded in it. Embedding is a map from the embedded surface to 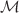that has a field theory described by Sigma model. I take d directions of 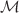to be the generators of a symmetry group SU(n) of the Lagrangian of the embedding. This means embedding has n flavors. Then I introduce spontaneous symmetry breaking in the theory and define the direction along which the symmetry breaking occurs as time. Next I write down the modified Einstein’s equation including the embedding. Then I discuss embedding’s relation to the expansion of the universe. After that I construct an inflationary scenario with embedding as inflaton and discuss its connection to Starobinsky 
model. Finally, I discuss the effect of inflation on the non-commutativity of the spacetime.
© The Author(s) 2021
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
