https://doi.org/10.1140/epjc/s10052-020-08788-w
Regular Article – Theoretical Physics
On perturbation theory and critical exponents for self-similar systems
Scuola Normale Superiore and I.N.F.N, Piazza dei Cavalieri 7, 56126, Pisa, Italy
Received:
13
October
2020
Accepted:
20
December
2020
Published online:
12
January
2021
Gravitational critical collapse in the Einstein-axion-dilaton system is known to lead to continuous self-similar solutions characterized by the Choptuik critical exponent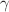 
. We complete the existing literature on the subject by computing the linear perturbation equations in the case where the axion-dilaton system assumes a parabolic form. Next, we solve the perturbation equations in a newly discovered self-similar solution in the hyperbolic case, which allows us to extract the Choptuik exponent. Our main result is that this exponent depends not only on the dimensions of spacetime but also the particular ansatz and the critical solutions that one started with.
The original online version of this article was revised: The author Ehsan Hatefi has only one affiliation: Scuola Normale Superiore and I.N.F.N, Piazza dei Cavalieri 7, 56126 Pisa, Italy.
An erratum to this article is available online at https://doi.org/10.1140/epjc/s10052-022-10084-8.
Copyright comment corrected publication 2022
© The Author(s) 2021. corrected publication 2022
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
