Eur. Phys. J. C (2025) 85: 815
https://doi.org/10.1140/epjc/s10052-025-14489-z

Review

Quantum gravity from Weyl conformal geometry

Department of Theoretical Physics, National Institute of Physics and Nuclear Engineering (IFIN), 077125, Bucharest, Romania

^a dumitru.ghilencea@cern.ch https://inspirehep.net/authors/1008499

Received: 19 June 2025
Accepted: 2 July 2025
Published online: 29 July 2025

Abstract

We review recent developments in physical implications of Weyl conformal geometry. The associated Weyl quadratic gravity action is a gauge theory of the Weyl group of dilatations and Poincaré symmetry. Weyl conformal geometry is defined by equivalence classes of the metric and Weyl gauge field (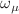${\omega }_{\mu }$), related by Weyl gauge transformations. Weyl geometry can be seen as a covariantised version of Riemannian geometry with respect to Weyl gauge symmetry (of dilatations). This Weyl gauge-covariant formulation of Weyl geometry is metric, which avoids century-old criticisms on the physical relevance of this geometry, that ignored its gauge symmetry. Weyl quadratic gravity and its geometry have interesting properties: (a) Weyl gauge symmetry is spontaneously broken and Einstein–Hilbert gravity and Riemannian geometry are recovered, with 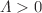$\mathrm{\Lambda }>0$; (b) this is the only true gauge theory of a space-time symmetry i.e. with a physical (Weyl) gauge boson (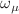${\omega }_{\mu }$); (c) all fields and masses have geometric origin (with no added scalar fields); (d) the theory has a Weyl gauge invariant geometric regularisation (by 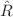$\widehat{R}$) in d dimensions and it is Weyl-anomaly free; this anomaly is recovered in the broken phase after massive 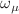${\omega }_{\mu }$ decouples; (e) the theory is the leading order of the general Weyl gauge invariant Dirac-Born–Infeld (WDBI) action of Weyl conformal geometry in d dimensions; (f) in the limit of vanishing Weyl gauge current, one obtains conformal gravity; (g) finally, Standard Model (SM) has a natural embedding in conformal geometry with no new degrees of freedom, with successful Starobinsky–Higgs inflation. Briefly, Weyl conformal geometry generates a (quantum) gauge theory of gravity, given by Weyl quadratic gravity action and its WDBI generalisation, and leads to a unified description, by the gauge principle, of Einstein–Hilbert gravity and SM interactions.