https://doi.org/10.1140/epjc/s10052-025-14481-7
Regular Article - Theoretical Physics
The problem of reconstruction for static spherically-symmetric 4D metrics in scalar-Einstein–Gauss–Bonnet model
1
Institute of Gravitation and Cosmology, Peoples’ Friendship University of Russia (RUDN University), 6 Miklukho-Maklaya Street, 117198, Moscow, Russian Federation
2
Center for Gravitation and Fundamental Metrology, Scientific Research Center of Applied Metrology Rostest, 46 Ozyornaya Street, 119361, Moscow, Russian Federation
Received:
5
March
2025
Accepted:
30
June
2025
Published online:
9
July
2025
We consider the 4D gravitational model with a scalar field  , Einstein and Gauss–Bonnet terms. The action of the model contains a potential term
, Einstein and Gauss–Bonnet terms. The action of the model contains a potential term 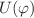 , Gauss–Bonnet coupling function
, Gauss–Bonnet coupling function 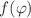 and a parameter
and a parameter 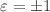 , where
, where 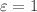 corresponds to ordinary scalar field and
corresponds to ordinary scalar field and 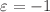 - to phantom one. Inspired by the recent works of Nojiri and Nashed, we explore a reconstruction procedure for a generic static spherically symmetric metric written in the Buchdal parametrization:
- to phantom one. Inspired by the recent works of Nojiri and Nashed, we explore a reconstruction procedure for a generic static spherically symmetric metric written in the Buchdal parametrization: 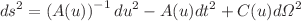 , with given
, with given  and
and 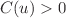 . The procedure gives the relations for
. The procedure gives the relations for 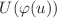 ,
,  and
and 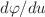 , which lead to exact solutions to equations of motion with a given metric. A key role in this approach is played by the solutions to a second order linear differential equation for the function
, which lead to exact solutions to equations of motion with a given metric. A key role in this approach is played by the solutions to a second order linear differential equation for the function  . The formalism is illustrated by two examples when: a) the Schwarzschild metric and b) the Ellis wormhole metric, are chosen as a starting point. For the first case a) the black hole solution with a “trapped ghost” is found which describes an ordinary scalar field outside the photon sphere and phantom scalar field inside the photon sphere. For the second case b) the sEGB-extension of the Ellis wormhole solution is found when the coupling function reads:
. The formalism is illustrated by two examples when: a) the Schwarzschild metric and b) the Ellis wormhole metric, are chosen as a starting point. For the first case a) the black hole solution with a “trapped ghost” is found which describes an ordinary scalar field outside the photon sphere and phantom scalar field inside the photon sphere. For the second case b) the sEGB-extension of the Ellis wormhole solution is found when the coupling function reads: 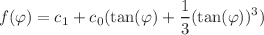 , where
, where  and
and 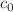 are constants.
are constants.
© The Author(s) 2025
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.




