https://doi.org/10.1140/epjc/s10052-024-13248-w
Regular Article - Theoretical Physics
Topological charges via Barrow entropy of black hole in metric-affine gravity
1
Department of Mathematics, Shanghai University and Newtouch Center for Mathematics of Shanghai University, 200444, Shanghai, People’s Republic of China
2
Department of Mathematics, COMSATS University Islamabad, Lahore-Campus, 54000, Lahore, Pakistan
3
Institute for Theoretical Physics and Cosmology, Zhejiang University of Technology, 310023, Hangzhou, People’s Republic of China
Received:
1
May
2024
Accepted:
21
July
2024
Published online:
19
September
2024
This paper examines distinct ensembles such as canonical, mixed, and grand canonical ensembles of recently postulated black hole which is considered to be an ideal solution of metric-affine gravity utilizing the Duan’s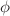 
-mapping theory. In the scenario, charged and uncharged topological characteristics associated to thermodynamic stability criteria are explored. In contrast to the canonical ensemble, which is always possesses the constant electric and magnetic charges, but mixed ensemble possesses the constant potentials (both magnetic and electric). Also, grand canonical ensemble maintains the constant electric and magnetic potentials for both charges. Initially, we find the topological classes connected via critical points in all of the aforementioned ensembles.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
