Possible wormholes in f(R) gravity sourced by solitonic quantum wave and cold dark matter halos and their repulsive gravity effect

Abdelghani Errehymy; Youssef Khedif; Orhan Donmez; Mohammed Daoud; Kairat Myrzakulov; Sabit Bekov

doi:10.1140/epjc/s10052-024-13224-4

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2024) 84: 908
https://doi.org/10.1140/epjc/s10052-024-13224-4

Regular Article – Theoretical Physics

Possible wormholes in f(R) gravity sourced by solitonic quantum wave and cold dark matter halos and their repulsive gravity effect

Abdelghani Errehymy¹^a, Youssef Khedif², Orhan Donmez³, Mohammed Daoud⁴^,5, Kairat Myrzakulov⁶^e and Sabit Bekov⁶^,7

¹ Astrophysics Research Centre, School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Private Bag X54001, 4000, Durban, South Africa
² Laboratory of High Energy and Condensed Matter Physics, Department of Physics, Faculty of Sciences Aïn Chock, University Hassan II, P.O. Box 5366, Maarif, 20100, Casablanca, Morocco
³ College of Engineering and Technology, American University of the Middle East, 54200, Egaila, Kuwait
⁴ Department of Physics, Faculty of Sciences, Ibn Tofail University, P.O. Box 133, 14000, Kenitra, Morocco
⁵ Abdus Salam International Centre for Theoretical Physics, 34151, Miramare, Trieste, Italy
⁶ Department of General and Theoretical Physics, L.N. Gumilyov Eurasian National University, 010008, Astana, Kazakhstan
⁷ Kozybayev University, 150000, Petropavlovsk, Kazakhstan

^a abdelghani.errehymy@gmail.com
^e krmyrzakulov@gmail.com

Received: 2 May 2024
Accepted: 9 August 2024
Published online: 6 September 2024

Abstract

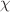In this paper, we present new generalized wormhole (WH) solutions within the context of f(R) gravity. Specifically, we focus on f(R) gravitational theories formulated in the metric formalism, with our investigation centered on a power-law form represented by $f (R) = ϵ R^{χ}$ $f(R) = \epsilon R^{\chi }$ . Here, $ϵ$ $\epsilon$ is an arbitrary constant, and $χ$ $\chi$ is a real number. Notably, this form possesses the advantageous property of reducing to Einstein gravity when 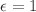$ϵ = 1$ $\epsilon =1$ and $χ = 1$ $\chi =1$ . 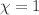To obtain these novel WH solutions, we establish the general field equations for any f(R) theory within the framework of Morris–Thorne spacetime, assuming metric coefficients that are independent of time. By utilizing an anisotropic matter source and a specific type of energy density associated with solitonic quantum wave (SQW) and cold dark matter (CDM) halos, we calculate two distinct WH solutions. We thoroughly investigate the properties of the exotic matter (ExoM) residing within the WH geometry and analyze the matter contents through energy conditions (ECs). Both analytical and graphical methods are employed in this analysis to examine the validity of different regions. Notably, the calculated shape functions for the WH geometry satisfy the necessary conditions in both scenarios, emphasizing their reliability. Our investigations into specific parameter ranges in both scenarios revealed the presence of ExoM. This ExoM is characterized by an energy–momentum tensor that violates the null energy condition (NEC) and, consequently, the weak energy condition as well, in the vicinity of the WH throats. Furthermore, we investigated the repulsive effect of gravity and discovered that its presence results in a negative deflection angle for photons following null geodesics. Importantly, we observed that the deflection angle consistently exhibits negative values across all 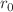$r_{0}$ $$r_0$$ values in both scenarios, indicating the manifestation of the repulsive gravity effect. Finally, we compare the obtained WH solutions utilizing both distributions, as well as the f(R) power-law-like models, in order to assess the feasibility of energetic configurations for WHs within SQW and CDM systems.

© The Author(s) 2024

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.