Self-interacting scalar field in (2+1) dimensions Einstein gravity with torsion

R. Kaya; H. T. Özçelik

doi:10.1140/epjc/s10052-024-12912-5

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2024) 84: 528
https://doi.org/10.1140/epjc/s10052-024-12912-5

Regular Article - Theoretical Physics

Self-interacting scalar field in (2+1) dimensions Einstein gravity with torsion

R. Kaya^a and H. T. Özçelik

Department of Physics, Yildiz Technical University, 34220, Istanbul, Davutpaşa, Turkey

^a rkaya@yildiz.edu.tr

Received: 21 October 2023
Accepted: 15 May 2024
Published online: 24 May 2024

Abstract

We study a massless real self-interacting scalar field 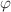$φ$ $\varphi$ non-minimally coupled to Einstein gravity with torsion in (2+1) space-time dimensions in the presence of a cosmological constant. The field equations with a self-interaction potential 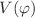$V (φ)$ $V(\varphi )$ including 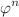$φ^{n}$ $\varphi ^{n}$ terms are derived by a variational principle. By numerically solving these field equations with the 4th Runge–Kutta method, the circularly symmetric rotating solutions for (2+1) dimensions Einstein gravity with torsion are obtained. Exact analytical solutions to the field equations are derived for the proposed metric in the absence of both torsion and angular momentum. We find that the self-interacting potential only exists for 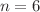$n = 6$ $$n=6$$ , as requested by conformal symmetry. We also study the motion of massive and massless particles in (2+1) Einstein gravity with torsion coupled to a self-interacting scalar field. The effect of torsion on the behavior of the effective potentials of the particles is analyzed numerically.

© The Author(s) 2024

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.