https://doi.org/10.1140/epjc/s10052-024-12755-0
Letter - Theoretical Physics
Exact phonon quasibound states around an optical black hole
Department of Physics, Mahidol University, 272 Phraram 6 Street, Ratchathewi, 10400, Bangkok, Thailand
Received:
19
February
2024
Accepted:
1
April
2024
Published online:
12
April
2024
In this work, we present an exact solution of phonon quasibound states in a vortex photon flow that creates an analogous black hole background. We worked out and successfully solve the governing differential equation of the systen that is similar with the relativistic Klein–Gordon equation. The exact radial solutions are discovered in terms of the confluent Heun functions that behaves as ingoing waves near the black hole’s horizon and decaying far away from the black hole’s horizon. The polynomial condition of the confluent Heun function leads to the discovery of the the complex valued quantized energy levels expression of the quasibound state of which depends on the phonon mass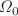 
, the photon vortex horizon’s spin 
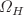and the azimuthal and the main quantum number (m, n). In the last section, by using the Damour–Ruffini method, the Hawking radiation of the analog black hole’s horizon is investigated to derive the phononic radiation distribution function from where, the Hawking temberature is obtained.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
