https://doi.org/10.1140/epjc/s10052-024-12707-8
Regular Article - Theoretical Physics
Worldline path integral for the massive graviton
1
Dipartimento di Fisica e Astronomia “Augusto Righi”, Università di Bologna, via Irnerio 46, 40126, Bologna, Italy
2
INFN, Sezione di Bologna, via Irnerio 46, 40126, Bologna, Italy
Received:
23
February
2024
Accepted:
20
March
2024
Published online:
30
March
2024
We compute the counterterms necessary for the renormalization of the one-loop effective action of massive gravity from a worldline perspective. This is achieved by employing the recently proposed massive 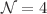 spinning particle model to describe the propagation of the massive graviton on those backgrounds that solve the Einstein equations without cosmological constant, namely on Ricci-flat manifolds, in four dimensions. The model is extended to be consistent in D spacetime dimensions by relaxing the gauging of the full SO(4) R-symmetry group to a parabolic subgroup, together with the inclusion of a suitable Chern–Simons term. Then, constructing the worldline path integral on the one-dimensional torus allows for the correct calculation of the one-loop divergencies in arbitrary D dimensions. Our primary contribution is the determination of the Seleey–DeWitt coefficients up to the fourth coefficient
spinning particle model to describe the propagation of the massive graviton on those backgrounds that solve the Einstein equations without cosmological constant, namely on Ricci-flat manifolds, in four dimensions. The model is extended to be consistent in D spacetime dimensions by relaxing the gauging of the full SO(4) R-symmetry group to a parabolic subgroup, together with the inclusion of a suitable Chern–Simons term. Then, constructing the worldline path integral on the one-dimensional torus allows for the correct calculation of the one-loop divergencies in arbitrary D dimensions. Our primary contribution is the determination of the Seleey–DeWitt coefficients up to the fourth coefficient  , which to our knowledge has never been reported in the literature. Its calculation is generally laborious on the quantum field theory side, as a general formula for these coefficients is not available for operators that are non-minimal in the heat kernel sense. This work illustrates the computational efficiency of worldline methods in this regard. Heat kernel coefficients characterize linearized massive gravity in a gauge-independent manner due to the on-shell condition of the background on which the graviton propagates. They could serve as a benchmark for verifying alternative approaches to massive gravity, and, for this reason, their precise expression should be known explicitly.
, which to our knowledge has never been reported in the literature. Its calculation is generally laborious on the quantum field theory side, as a general formula for these coefficients is not available for operators that are non-minimal in the heat kernel sense. This work illustrates the computational efficiency of worldline methods in this regard. Heat kernel coefficients characterize linearized massive gravity in a gauge-independent manner due to the on-shell condition of the background on which the graviton propagates. They could serve as a benchmark for verifying alternative approaches to massive gravity, and, for this reason, their precise expression should be known explicitly.
© The Author(s) 2024
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.




