https://doi.org/10.1140/epjc/s10052-024-12432-2
Regular Article - Experimental Physics
Explicit near-symplectic integrators for post-Newtonian Hamiltonian systems
1
School of Mathematics, Yunnan Normal University, 650500, Kunming, China
2
Yunnan Key Laboratory of Modern Analytical Mathematics and Applications, Yunnan Normal University, 650500, Kunming, China
3
Purple Mountain Observatory, Chinese Academy of Sciences, 210023, Nanjing, China
4
School of Astronomy and Space Science, University of Science and Technology of China, 230026, Hefei, China
Received:
5
October
2023
Accepted:
11
January
2024
Published online:
24
January
2024
Explicit symplectic integrators are powerful and widely used for Hamiltonian systems. However, once the post-Newtonian (PN) effect is considered to provide more precise modeling for the N-body problem, explicit symplectic methods cannot be constructed due to the nonseparability of the Hamiltonian. Thus, the available symplectic method is either fully implicit or semi-implicit, which decreases the efficiency because of the implicit iteration used during the evolution. In this paper, we aim to explore efficient explicit methods whose performance is mostly like symplectic methods for PN Hamiltonian systems. Taking the small parameter  appearing in PN terms into consideration, we replace the implicit symplectic solver with explicit solvers in the mixed symplectic method to solve the PN term and then derive three explicit methods. It is theoretically shown that the proposed methods are respectively second-order, fourth-order, and pseudo-fourth-order, and that their closeness to the corresponding symplectic methods are
appearing in PN terms into consideration, we replace the implicit symplectic solver with explicit solvers in the mixed symplectic method to solve the PN term and then derive three explicit methods. It is theoretically shown that the proposed methods are respectively second-order, fourth-order, and pseudo-fourth-order, and that their closeness to the corresponding symplectic methods are 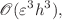
 and
and 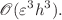 That is, they are explicit near-symplectic methods with the presence of the small parameter
That is, they are explicit near-symplectic methods with the presence of the small parameter  Numerical experiments with the Hamiltonian problem of spinning compact binaries show that the energy errors and orbital errors of the proposed explicit near-symplectic methods are indistinguishable from the corresponding mixed semi-implicit symplectic methods. The very small magnitude of the difference between the proposed explicit near-symplectic methods and the mixed symplectic methods confirms our theoretical analysis of their closeness to symplecticity. Finally, the much less CPU time consumed by the proposed methods highlights their most important advantage of high efficiency over the mixed symplectic methods.
Numerical experiments with the Hamiltonian problem of spinning compact binaries show that the energy errors and orbital errors of the proposed explicit near-symplectic methods are indistinguishable from the corresponding mixed semi-implicit symplectic methods. The very small magnitude of the difference between the proposed explicit near-symplectic methods and the mixed symplectic methods confirms our theoretical analysis of their closeness to symplecticity. Finally, the much less CPU time consumed by the proposed methods highlights their most important advantage of high efficiency over the mixed symplectic methods.
© The Author(s) 2024
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.




