https://doi.org/10.1140/epjc/s10052-023-12255-7
Regular Article - Theoretical Physics
A class of rotating metrics in the presence of a scalar field
Department of Physics, Isfahan University of Technology, 84156-83111, Isfahan, Iran
a
b.mirza@iut.ac.ir
c
fatemeh.sadeghi96@ph.iut.ac.ir
Received:
30
July
2023
Accepted:
13
November
2023
Published online:
20
December
2023
We consider a class of three parameter static and axially symmetric metrics that reduce to the Janis–Newman–Winicour (JNW) and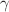 
-metrics in certain limits of the parameters. We obtain rotating form of the metrics that are asymptotically flat, stationary and axisymmetric. In certain values of the parameters, the solutions represent the rotating JNW metric, rotating 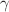-metric and Bogush–Gal’tsov (BG) metric. The singularities of rotating metrics are investigated. Using the light-ring method, we obtain the quasi normal modes (QNMs) related to rotating metrics in the eikonal limit. Finally, we investigate the precession frequency of a test gyroscope in the presence of the rotating metrics.
© The Author(s) 2023
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
