https://doi.org/10.1140/epjc/s10052-023-11943-8
Regular Article - Theoretical Physics
Flow of shear response functions in hyperscaling violating Lifshitz theories
1
National Institute of Theoretical and Computational Sciences, School of Physics and Mandelstam Institute for Theoretical Physics, University of the Witwatersrand, Wits, 2050, Johannesburg, South Africa
2
Department of Physics, Indian Institute of Technology Kanpur, 208016, Kanpur, India
3
School of Physics, IISER Thiruvananthapuram, 695551, Thiruvananthapuram, India
a
arghya.chattopadhyay@wits.ac.za
Received:
24
June
2023
Accepted:
19
August
2023
Published online:
31
August
2023
We study the flow equations of the shear response functions for hyperscaling violating Lifshitz (hvLif) theories, with Lifshitz and hyperscaling violating exponents z and 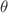 . Adapting the membrane paradigm approach of analysing response functions as developed by Iqbal and Liu, we focus specifically on the shear gravitational modes which now are coupled to the perturbations of the background gauge field. Restricting to the zero momenta sector, we make further simplistic assumptions regarding the hydrodynamic expansion of the perturbations. Analysing the flow equations shows that the shear viscosity at leading order saturates the Kovtun–Son–Starinets (KSS) bound of
. Adapting the membrane paradigm approach of analysing response functions as developed by Iqbal and Liu, we focus specifically on the shear gravitational modes which now are coupled to the perturbations of the background gauge field. Restricting to the zero momenta sector, we make further simplistic assumptions regarding the hydrodynamic expansion of the perturbations. Analysing the flow equations shows that the shear viscosity at leading order saturates the Kovtun–Son–Starinets (KSS) bound of 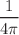 . When
. When  , (
, (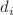 being the number of spatial dimension in the dual field theory) the first-order correction to shear viscosity exhibits logarithmic scaling, signalling the emergence of a scale in the UV regime for this class of hvLif theories. We further show that the response function associated to the gauge field perturbations diverge near the boundary when
being the number of spatial dimension in the dual field theory) the first-order correction to shear viscosity exhibits logarithmic scaling, signalling the emergence of a scale in the UV regime for this class of hvLif theories. We further show that the response function associated to the gauge field perturbations diverge near the boundary when 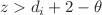 . This provides a holographic understanding of the origin of such a constraint and further vindicates results obtained in previous works that were obtained through near horizon and quasinormal mode analysis.
. This provides a holographic understanding of the origin of such a constraint and further vindicates results obtained in previous works that were obtained through near horizon and quasinormal mode analysis.
Nihal M: Majority of the work was done while the author was affiliated to: School of Physics, IISER Thiruvananthapuram, Thiruvananthapuram, 695551, India.
© The Author(s) 2023
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.




