Confront modified gravity with the massive pulsar

G. G. L. Nashed

doi:10.1140/epjc/s10052-023-11882-4

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2023) 83: 698
https://doi.org/10.1140/epjc/s10052-023-11882-4

Regular Article - Theoretical Physics

Confront $f (R, T) = R + β T$ $f(R,T)={\mathcal {R}}+\beta T$ modified gravity with the massive pulsar $PSR J 0740 + 6620$ ${\textit{PSR J0740+6620}}$

G. G. L. Nashed^a

Centre for Theoretical Physics, The British University in Egypt, P.O. Box 43, 11837, El Sherouk City, Cairo, Egypt

^a nashed@bue.edu.eg

Received: 8 June 2023
Accepted: 28 July 2023
Published online: 7 August 2023

Abstract

Many physically inspired general relativity (GR) modifications predict significant deviations in the properties of spacetime surrounding massive neutron stars. Among these modifications is 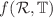$f (R, T)$ $f({\mathcal {R}}, {\mathbb {T}})$ , where 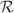$R$ ${\mathcal {R}}$ is the Ricci scalar, $T$ ${\mathbb {T}}$ is the trace of the energy–momentum tensor, the gravitational theory that is thought to be a neutral extension of GR. 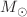Neutron stars with masses above 1.8 $M_{⊙}$ $M_{\odot }$ expressed as radio pulsars are precious tests of fundamental physics in extreme conditions unique in the observable universe and unavailable to terrestrial experiments. 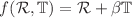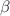We obtained an exact analytical solution for anisotropic perfect-fluid spheres in hydrostatic equilibrium using the frame of the linear form of $f (R, T) = R + β T$ $f({\mathcal {R}},{\mathbb {T}})={\mathcal {R}}+\beta {\mathbb {T}}$ where $β$ $\beta$ is a dimensional parameter. We show that the dimensional parameter 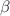$β$ $\beta$ and the compactness, $C = \frac{2 G M}{R c^{2}}$ $C=\frac{2GM}{Rc^2}$ can be used to express all physical quantities within the star. We fix the dimensional parameter 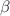$β$ $\beta$ to be at most 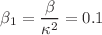$β_{1} = \frac{β}{κ^{2}} = 0.1$ $\beta _1=\frac{\beta }{\kappa ^2}= 0.1$ in positive values through the use of observational data from NICER and X-ray Multi-Mirror telescopes on the pulsar $PSR J 0740 + 6620$ ${\textit{PSR J0740+6620}}$ , which provide information on its mass and radius. The mass and radius of the pulsar $PSR J 0740 + 6620$ ${\textit{PSR J0740+6620}}$ were determined by analyzing data obtained from NICER and X-ray Multi-Mirror telescopes. It is important to mention that no assumptions about equations of state were made in this research. Nevertheless, the model demonstrates a good fit with linear patterns involving bag constants. 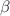Generally, when the dimensional parameter $β$ $\beta$ is positive, the theory predicts that a star of the same mass will have a slightly larger size than what is predicted by GR. It has been explained that the hydrodynamic equilibrium equation includes an additional force resulting from the coupling between matter and geometry. This force partially reduces the effect of gravitational force. As a result, we compute the maximum compactness allowed by the strong energy condition for 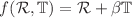$f (R, T) = R + β T$ $f({\mathcal {R}}, {\mathbb {T}})={\mathcal {R}}+\beta {\mathbb {T}}$ and for GR, which are $C = 0.757$ $$C = 0.757$$ and 0.725, respectively. These values are approximately 3% higher than the prediction made by GR.. 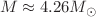Furthermore, we estimate the maximum mass $M \approx 4.26 M_{⊙}$ $M\approx 4.26 M_{\odot }$ at a radius of 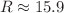$R \approx 15.9$ $R\approx 15.9$ km for the surface density at saturation nuclear density 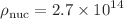$ρ_{nuc} = 2.7 \times 10^{14}$ $\rho _{\text {nuc}} = 2.7\times 10^{14}$ g/cm $^{3}$ $$^3$$ .

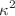Here $κ^{2}$ ${\kappa ^2}$ is the coupling constant of Einstein which is figured as $κ^{2} = \frac{8 π G}{c^{4}}$ ${\kappa ^2=\frac{8\pi G}{c^4}}$ , the Newtonian constant of gravitation is denoted as $F$ ${\textrm{F}}$ while $c$ ${\textrm{c}}$ represents the speed of light.

© The Author(s) 2023

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Funded by SCOAP³. SCOAP³ supports the goals of the International Year of Basic Sciences for Sustainable Development.

Conference announcements

International Conference on Phenomena in Ionized Gases
June 20-27, 2025
Aix-en-Provence, France

15th European Conference on Atoms Molecules and Photons (ECAMP)
June 30 to July 4, 2025
Innsbruck, Austria

Joint Annual Meeting of ÖPG and SPS
August 18-22, 2025
Wien, Austria

111th Italian National Society Congress
September 22-26, 2025
Palermo, Italy

EPJ

Confront f(R,T)=R+βT modified gravity with the massive pulsar PSR J0740+6620

Conference announcements

Confront $f (R, T) = R + β T$ $f(R,T)={\mathcal {R}}+\beta T$ modified gravity with the massive pulsar $PSR J 0740 + 6620$ ${\textit{PSR J0740+6620}}$