https://doi.org/10.1140/epjc/s10052-022-10688-0
Regular Article - Theoretical Physics
A novel definition of complexity in torsion based theory
Department of Mathematics, University of the Punjab, Quaid-i-Azam Campus, 54590, Lahore, Pakistan
Received:
14
July
2022
Accepted:
7
August
2022
Published online:
17
August
2022
Despite coming across quite effective definitions of complexity in terms of many modified theories of gravity, it still has a question about its existence in f(T) gravity, where the torsion scalar T is accountable for gravitational impacts. The emergence of complexity factor is due to division of intrinsic curvature in an orthogonal way as described by Herrera (Phys Rev D 97:044010, 2018). To initiate the analysis, we reckon the interior region is like a spherically symmetric static configuration filled by the locally anisotropic fluid and exteriorly associated with a spherical hypersurface. In this framework, we acquire the f(T) field equations and utilize the already formulated relationship between the intrinsic curvature and the conformal tensor to perform our analysis. We bring into action the definitions of the two frequently availed masses (Tolman and Misner–Sharp) for spherical composition and investigate the appealing correlation between them and the conformal tensor. The impact of the local anisotropy and the homogeneity and inhomogeneity of energy density has substantial importance in this regard. We build up some relation in terms of already defined variables and interpret the complexity as a single scalar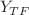 
. It deduce that this factor vanished when the fluid content is homogenous and also when the impact of two anisotropic terms cancel out in the case of inhomogeneous fluid content. We determine a few definite interior solutions which fulfill the criterion of vanishing scalar 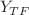. Certain defined ideas in fulfillment of the vanishing complexity factor constraint, are applied for f(T) gravity.
© The Author(s) 2022
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
