https://doi.org/10.1140/epjc/s10052-022-10074-w
Regular Article - Theoretical Physics
Islands in Kaluza–Klein black holes
School of Physics, Huazhong University of Science and Technology, 430074, Wuhan, Hubei, China
Received:
1
September
2021
Accepted:
30
January
2022
Published online:
11
February
2022
The newly proposed island formula for entanglement entropy of Hawking radiation is applied to spherically symmetric 4-dimensional eternal Kaluza–Klein (KK) black holes. The “charge” Q of KK black holes quantifies its deviation from Schwarzschild black holes. The impact of Q on the island is studied at late times. The late-time island, whose boundary is located outside but within a Planckian distance of the horizon, is slightly extended by Q. While the no-island entropy grows linearly, the late-time entanglement entropy is given by island configuration with twice the Bekenstein–Hawking entropy. Thus we reproduce the Page curve for the eternal KK black holes. Compared with Schwarzschild results, the Page time is delayed by a factor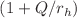 
and the scrambling time is prolonged by a factor 
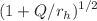. Moreover, the higher-dimensional generalization is presented. Skeptically, there are Planck length scales involved, in which a semi-classical description may break down.
© The Author(s) 2022
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
