https://doi.org/10.1140/epjc/s10052-019-7369-0
Regular Article - Theoretical Physics
Salient features of dressed elliptic string solutions on 
1
Department of Physics, National and Kapodistrian University of Athens, University Campus, Zografou, 15784, Athens, Greece
2
Institute of Nuclear and Particle Physics, NCSR “Demokritos”, Agia Paraskevi, 15310, Attiki, Greece
3
Department of Physics, School of Applied Mathematics and Physical Sciences, National Technical University, 15780, Athens, Greece
* e-mail: pastras@inp.demokritos.gr
Received:
26
August
2019
Accepted:
2
October
2019
Published online:
23
October
2019
We study several physical aspects of the dressed elliptic strings propagating on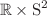 
and of their counterparts in the Pohlmeyer reduced theory, i.e. the sine-Gordon equation. The solutions are divided into two wide classes; kinks which propagate on top of elliptic backgrounds and non-localised periodic disturbances of the latter. The former class of solutions obey a specific equation of state that is in principle experimentally verifiable in systems which realize the sine-Gordon equation. Among both of these classes, there appears to be a particular class of interest the closed dressed strings. They in turn form four distinct subclasses of solutions. One of those realizes instabilities of the seed elliptic solutions. The existence of such solutions depends on whether a superluminal kink with a specific velocity can propagate on the corresponding elliptic sine-Gordon solution. Unlike the elliptic strings, the dressed ones exhibit interactions among their spikes. These interactions preserve an appropriately defined turning number, which can be associated to the topological charge of the sine-Gordon counterpart. Finally, the dispersion relations of the dressed strings are studied. A qualitative difference between the two wide classes of dressed strings is discovered.
© The Author(s), 2019
