https://doi.org/10.1140/epjc/s10052-019-7250-1
Regular Article - Theoretical Physics
Conductivity of the holographic p-wave superconductors with higher order corrections
1
Physics Department and Biruni Observatory, Shiraz University, Shiraz, 71454, Iran
2
Research Institute for Astronomy and Astrophysics of Maragha (RIAAM), P. O. Box: 55134-441, Maragha, Iran
* e-mail: asheykhi@shirazu.ac.ir
Received:
12
July
2019
Accepted:
12
August
2019
Published online:
6
September
2019
We investigate the holographic p-wave superconductors in the presence of the higher order corrections on the gravity as well as on the gauge field side. On the gravity side, we add the Gauss–Bonnet curvature correction terms, while on the gauge field side we take the nonlinear Lagrangian in the form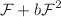 
, where 
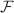is the Maxwell Lagrangian and b indicates the strength of the nonlinearity. We employ the shooting method for the numerical calculations in order to obtain the ratio of the critical temperature 
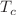over 
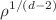. We observe that by increasing the values of the mass and the nonlinear parameters the critical temperature decreases and thus the condensation becomes harder to form. In addition, the stronger Gauss–Bonnet parameter 
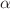hinders the superconducting phase in Gauss–Bonnet gravity. Furthermore, we calculate the electrical conductivity based on the holographic setup. The real and imaginary parts are related by the Kramers–Kronig relation, which indicates a delta function and a pole in low frequency regime, respectively. However, at enough large frequencies the trend of the real part can be interpreted by 
. Moreover, in holographic model the ratio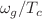 
is always much larger than the BCS value 3.5 due to the strong coupling of holographic superconductors. In both kinds of gravity, decreasing the temperature or increasing the effect of nonlinearity shifts the gap frequency toward larger values. Besides, the gap frequency occurred at larger values by enlarging the Gauss–Bonnet parameter. In general, the behavior of the conductivity depends on the choice of the mass, the nonlinear and the Gauss–Bonnet parameters.
© The Author(s), 2019
