Eur. Phys. J. C (2008) 53: 429-446
https://doi.org/10.1140/epjc/s10052-007-0472-7

Regular Article - Theoretical Physics

Wedgebox analysis of four-lepton events from neutralino pair production at the LHC

¹ Center for High Energy Physics and Department of Physics, Tsinghua University, 100084, Beijing, P.R. China
² Physics Department, Sichuan University, 610064, Changdu, P.R. China

^* e-mail: bisset@mail.tsinghua.edu.cn

Received: 27 March 2007
Revised: 26 September 2007
Published online: 4 December 2007

Abstract

A ‘wedgebox’ plot is a two-dimensional scatter-plot of two invariant mass quantities. Here pp→e⁺e^-μ⁺μ^-+≠E signature LHC events are analyzed by plotting the di-electron invariant mass versus the di-muon invariant mass. Data sets of such events are obtained across the MSSM input parameter space in realistic event-generator simulations, including cuts designed to remove SM backgrounds. Their study reveals several general features. Firstly, regions in the MSSM input parameter space where a sufficient number of events are expected so as to be able to construct a clear wedgebox plot are delineated. Secondly, the presence of box shapes on a wedgebox plot either indicates the presence of heavy Higgs bosons’ decays or restricts the location to a quite small region of low μ and M₂ values, ≲ 200 GeV, a region denoted as the ‘lower island’. In this region, wedgebox plots can be quite complicated and change in pattern rather quickly as one moves around in the (μ,M₂) plane. Thirdly, direct neutralino pair production from an intermediate Z^0* may only produce a wedge shape since only decays can contribute significantly. And fourthly, a double-wedge or wedge-protruding-from-a-box pattern on a wedgebox plot, which results from combining a variety of MSSM production processes, yields three distinct observed endpoints, almost always attributable to 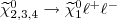decays, which can be utilized to determine a great deal of information about the neutralino and slepton mass spectra and related MSSM input parameters. Wedge and double-wedge patterns are seen in wedgebox plots in another region of higher μ and M₂ values, denoted as the ‘upper island’. Here the pattern is simpler and more stable as one moves across the (μ,M₂) input parameter space.