https://doi.org/10.1140/epjc/s10052-025-14590-3
Regular Article - Theoretical Physics
Apparent convergence in functional glueball calculations
1
Institut für Theoretische Physik, Justus-Liebig-Universität Giessen, Heinrich-Buff-Ring 16, 35392, Giessen, Germany
2
Helmholtz Forschungsakademie Hessen für FAIR (HFHF), GSI Helmholtzzentrum für Schwerionenforschung, Campus Gießen, 35392, Giessen, Germany
3
Silicon Austria Labs GmbH, Sandgasse 34, 8010, Graz, Austria
a
markus.huber@theo.physik.uni-giessen.de
Received:
7
March
2025
Accepted:
29
July
2025
Published online:
8
August
2025
We scrutinize the determination of glueball masses in pure Yang–Mills theory from functional equations, i.e. Dyson–Schwinger and Bethe–Salpeter equations. We survey the state-of-the-art input (dressed propagators and vertices) with an emphasis on the stability of the results under extensions of the employed truncations and explore the importance of different aspects of the bound state equations, focusing on the three lightest glueballs with 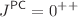 ,
,  and
and  . As an important systematic extension compared to previous calculations we include two-loop diagrams in the Bethe–Salpeter kernels. In terms of the glueball spectrum we find only marginal mass shifts compared to previous results, indicating apparent convergence of the system. As a by-product, we also explore gauge invariance within a class of Landau-type gauges.
. As an important systematic extension compared to previous calculations we include two-loop diagrams in the Bethe–Salpeter kernels. In terms of the glueball spectrum we find only marginal mass shifts compared to previous results, indicating apparent convergence of the system. As a by-product, we also explore gauge invariance within a class of Landau-type gauges.
© The Author(s) 2025
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.




