Eur. Phys. J. C (2025) 85: 751
https://doi.org/10.1140/epjc/s10052-025-14473-7

Regular Article - Theoretical Physics

Accurate critical exponents from the optimal truncation of the $\epsilon$-expansion within the O(N)-symmetric field theory for large N

Department of Physics and Materials Sciences, College of Arts and Sciences, Qatar University, Al Tarfa, 2713, Doha, Qatar

^a amshalab@qu.edu.qa

Received: 2 September 2024
Accepted: 26 June 2025
Published online: 8 July 2025

Abstract

The perturbation series for the renormalization group functions of the O(N)-symmetric 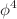${\varphi }^4$ field theory are divergent but asymptotic. They are usually followed by Resummation calculations to extract reliable results. Although the same features exist for QED series, their partial sums can return accurate results because the perturbation parameter is small. In this work, however, we show that, for 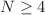$N\ge 4$, the partial sum (according to optimal truncation) of the series for the exponents $\nu$ and $\eta$ gives results that are very competitive to the recent Monte Carlo, Non-perturbative Renormalization group and Conformal field calculations. 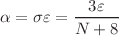The order at which the series is truncated is inversely proportional to $\alpha =\sigma \epsilon =\frac{3\epsilon }{N+8}$ which is higher for larger N while the error is smaller. Thus as N increases one expects accurate perturbative results like the QED case. Such optimal truncation, however, doesn’t work for the series of the critical exponent 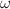$\omega$ (for intermediate values of N) as the truncated series includes only the first order. Nevertheless, for 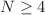$N\ge 4$, the large-order parameter 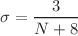$\sigma =\frac{3}{N+8}$ is getting smaller which rationalizes for the use of Pad$\acute{\text{e}}$ approximation. For that aim, we first obtain the seven-loop $\epsilon$-series from the recent available corresponding g-expansion. The seven-loop Pad$\acute{\text{e}}$ approximation gives accurate results for the three exponents. Besides, for all the seven orders in the series, the large-N limit leads to the exact result predicted by the non-perturbative 1/N-expansion.