https://doi.org/10.1140/epjc/s10052-025-14467-5
Regular Article - Theoretical Physics
Particles in finite volumes and a toy model of decaying neutrons
Atominstitut, Technische Universität Wien, Stadionallee 2, 1020, Vienna, Austria
a
christian.kaeding@tuwien.ac.at
Received:
6
May
2025
Accepted:
23
June
2025
Published online:
9
July
2025
It is well-known that the momentum spectra of particles confined to finite spatial volumes deviate from the continuous spectra used for unconfined particles. In this article, we consider real scalar particles confined to finite volumes with periodic boundary conditions, such that the particles’ spectra are discrete. We directly compute the density matrices describing the decay processes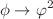 
and 
, and subsequently derive expressions for the decay probabilities both for confined and unconfined particles. The latter decay process is used as a rough toy model for a neutron decaying into a proton, an electron, and an anti-electron neutrino. We propose that finite volume effects can have an impact on the outcomes of experiments measuring the neutron lifetime. In addition, our findings at the toy model level suggest that taking into account possible initial correlations between neutrons and their daughter particles might be relevant as well.
© The Author(s) 2025
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
