https://doi.org/10.1140/epjc/s10052-025-14045-9
Regular Article - Theoretical Physics
Spin one matter fields
1
Departamento de Física, Universidade Federal de Viçosa, Campus Universitário, Avenida Peter Henry Rolfs s/n, 36570-900, Viçosa, MG, Brazil
2
, Praça Graccho Cardoso 76/504, 49015-180, Aracaju, SE, Brazil
Received:
27
November
2024
Accepted:
6
March
2025
Published online:
10
April
2025
It is shown how spin one vector matter fields can be coupled to a Yang–Mills theory. Such matter fields are defined as belonging to a representation R of this Yang–Mills gauge algebra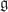 
. It is also required that these fields together with the original gauge fields be the gauge fields of an embedding total gauge algebra 
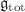. The existence of a physically consistent Yang–Mills action for the total algebra is finally required. These conditions are rather restrictive, as shown in some examples: non-trivial solutions may or may not exist depending on the choice of the original algebra 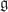and of the representation R. Some examples are shown, the case of the initial algebra = 
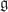being treated in more detail.
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1140/epjc/s10052-025-14045-9.
© The Author(s) 2025
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
