Eur. Phys. J. C (2024) 84: 1229
https://doi.org/10.1140/epjc/s10052-024-13590-z

Letter

Nonresonant renormalization scheme for twist-2 operators in SU(N) Yang–Mills theory

¹ Physics Department, INFN Roma1, Piazzale A. Moro 2, 00185, Rome, Italy
² Physics Department, Sapienza University, Piazzale A. Moro 2, 00185, Rome, Italy

^a francesco.scardino@uniroma1.it

Received: 22 October 2024
Accepted: 5 November 2024
Published online: 27 November 2024

Abstract

Recently, the short-distance asymptotics of the generating functional of n-point correlators of twist-2 operators in SU(N) Yang–Mills (YM) theory has been worked out in Bochicchio et al. (Phys Rev D 108:054023, 2023). 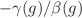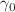The above computation relies on a basis change of renormalized twist-2 operators, where $-\gamma (g)/\beta (g)$ reduces to ${\gamma }_0/({\beta }_{0}g)$ to all orders of perturbation theory, with ${\gamma }_0$ diagonal, 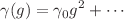$\gamma (g)={\gamma }_0{g}^2+\cdots$ the anomalous-dimension matrix and $\beta (g)=-{\beta }_0{g}^3+\cdots$ the beta function. 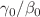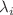The construction is based on a novel geometric interpretation of operator mixing (Bochicchio in Eur Phys J C 81:749, 2021), under the assumption that the eigenvalues of the matrix ${\gamma }_0/{\beta }_0$ satisfy the nonresonant condition ${\lambda }_i-{\lambda }_j\ne 2k$, with ${\lambda }_i$ in nonincreasing order and $k\in {\mathbb{N}}^{+}$. The nonresonant condition has been numerically verified up to 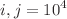$i,j={10}^4$ in Bochicchio et al. (Phys Rev D 108:054023, 2023). In the present paper we provide a number theoretic proof of the nonresonant condition for twist-2 operators essentially based on the classic result that Harmonic numbers are not integers. Our proof in YM theory can be extended with minor modifications to twist-2 operators in $\mathcal{N}=1$ SUSY YM theory, large-N QCD with massless quarks and massless QCD-like theories.