Eur. Phys. J. C (2024) 84: 1005
https://doi.org/10.1140/epjc/s10052-024-13418-w

Regular Article - Theoretical Physics

Finite distance effects on the Hellings–Downs curve in modified gravity

¹ Institute for Theoretical Physics, Leibniz University Hannover, Appelstraße 2, 30167, Hannover, Germany
² Max-Planck-Institut für Gravitationsphysik, Albert-Einstein-Institut, 30167, Hannover, Germany

^b apostolos.tsabodimos@stud.uni-hannover.de

Received: 13 August 2024
Accepted: 22 September 2024
Published online: 7 October 2024

Abstract

There is growing interest in the overlap reduction function in pulsar timing array observations as a probe of modified gravity. However, current approximations to the Hellings–Downs curve for subluminal gravitational wave propagation, say 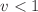$v<1$, diverge at small angular pulsar separation. In this paper, we find that the overlap reduction function for the 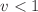$v<1$ case is sensitive to finite distance effects. First, we show that finite distance effects introduce an effective cut-off in the spherical harmonics decomposition at $\ell \sim \sqrt{1-v^2}kL$, where $\ell$ is the multipole number, k the wavenumber of the gravitational wave and L the distance to the pulsars. 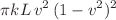Then, we find that the overlap reduction function in the small angle limit approaches a value given by $\pi kL{v}^2{(1-v^2)}^2$ times a normalization factor, exactly matching the value for the autocorrelation recently derived. Although we focus on the 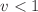$v<1$ case, our formulation is valid for any value of v.