https://doi.org/10.1140/epjc/s10052-024-13338-9
Regular Article - Theoretical Physics
Gravitational lensing and shadow by a Schwarzschild-like black hole in metric-affine bumblebee gravity
1
School of Physics and Electronic Science, Guizhou Normal University, 550001, Guiyang, Guizhou, People’s Republic of China
2
College of Physics, Nanjing University of Aeronautics and Astronautics, 211106, Nanjing, China
Received:
11
June
2024
Accepted:
4
September
2024
Published online:
27
September
2024
In this paper, we investigate the gravitational lensing effect and the shadow around a Schwarzschild-like black hole in metric-affine bumblebee gravity, which leads to the Lorentz symmetry breaking. We first present a generalized formalism for calculating higher-order corrections to light weak bending angle in a static, spherically symmetric and not asymptotically flat spacetime, and then applying this general formalism to the metric-affine bumblebee gravity. Moreover, we derive the light deflection angle and the size of the Einstein ring within the weak field in this scenario. In addition, we analyze the black hole shadow in this theory framework. By using observational data from the Einstein’s ring of the galaxy ESO325-G004 and the black hole shadow of the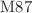 
galaxy, we estimate the upper bounds of the Lorentz symmetry breaking coefficient 
, respectively.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
