https://doi.org/10.1140/epjc/s10052-024-13297-1
Regular Article - Theoretical Physics
A hierarchy of WZW models related to super Poisson–Lie T-duality
Department of Physics, Faculty of Basic Sciences, Azarbaijan Shahid Madani University, 53714-161, Tabriz, Iran
Received:
24
June
2024
Accepted:
24
August
2024
Published online:
15
September
2024
Motivated by super Poisson–Lie (PL) symmetry of the Wess–Zumino–Witten (WZW) model based on the 
Lie supergroup of our previous work (Eghbali et al., in J High Energy Phys 07:134, 2013. arXiv:1303.4069 [hep-th]), we first obtain and classify all Drinfeld superdoubles (DSDs) generated by the Lie superbialgebra structures on the 
Lie superalgebra as a theorem. Then, introducing a general formulation we find the conditions under which a two-dimensional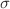 
-model may be equivalent to a WZW model. With the help of this formulation and starting the super PL symmetric WZW model, we get a hierarchy of WZW models related to super PL T-duality, in such a way that it is different from the super PL T-plurality, because the DSDs are, in this process, non-isomorphic. The most interesting indication of this work is that the WZW model does remain invariant under the super PL T-duality transformation, that is, the model is super PL self-dual.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
