https://doi.org/10.1140/epjc/s10052-024-13168-9
Regular Article – Theoretical Physics
Generalization of conformal Hamada operators
Departamento de Física, Instituto de Ciências Exatas, Universidade Federal de Juiz de Fora, 33036-900, Juiz de Fora, MG, Brazil
Received:
11
May
2024
Accepted:
26
July
2024
Published online:
19
September
2024
The six-derivative conformal scalar operator was originally found by Hamada in its critical dimension of spacetime,  . We generalize this construction to arbitrary dimensions d by adding new terms cubic in gravitational curvatures and by changing its coefficients of expansion in various curvature terms. The consequences of global scale-invariance and of infinitesimal local conformal transformations are derived for the form of this generalized operator. The system of linear equations for coefficients is solved giving explicitly the conformal Hamada operator in any d. Some singularities in construction for dimensions
. We generalize this construction to arbitrary dimensions d by adding new terms cubic in gravitational curvatures and by changing its coefficients of expansion in various curvature terms. The consequences of global scale-invariance and of infinitesimal local conformal transformations are derived for the form of this generalized operator. The system of linear equations for coefficients is solved giving explicitly the conformal Hamada operator in any d. Some singularities in construction for dimensions  and
and  are noticed. We also prove a general theorem that a scalar conformal operator with n derivatives in
are noticed. We also prove a general theorem that a scalar conformal operator with n derivatives in 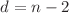 dimensions is impossible to construct. Finally, we compare our explicit construction with the one that uses conformal covariant derivatives and conformal curvature tensors. We present new results for operators built with different orders of conformal covariant derivatives.
dimensions is impossible to construct. Finally, we compare our explicit construction with the one that uses conformal covariant derivatives and conformal curvature tensors. We present new results for operators built with different orders of conformal covariant derivatives.
© The Author(s) 2024
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.




