Eur. Phys. J. C (2024) 84: 839
https://doi.org/10.1140/epjc/s10052-024-13091-z

Regular Article - Theoretical Physics

Counting 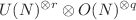$U{(N)}^{\otimes r}\otimes O{(N)}^{\otimes q}$ invariants and tensor model observables

¹ Okinawa Institute of Science and Technology Graduate University, 1919-1, Tancha, Onna, Kunigami District, 904-0495, Okinawa, Japan
² ICMPA-UNESCO Chair, 072BP50, Cotonou, Benin
³ Laboratoire Bordelais de Recherche en Informatique UMR CNRS 5800, Université de Bordeaux, 351 cours de la libération, 33522, Talence, France
⁴ Laboratoire d’Informatique de Paris Nord UMR CNRS 7030 Université Sorbonne Paris Nord, 99, avenue J.-B. Clement, 93430, Villetaneuse, France

^b bengeloun@lipn.univ-paris13.fr

Received: 4 June 2024
Accepted: 27 June 2024
Published online: 21 August 2024

Abstract

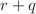$U{(N)}^{\otimes r}\otimes O{(N)}^{\otimes q}$ invariants are constructed by contractions of complex tensors of order $r+q$, also denoted (r, q). These tensors transform under r fundamental representations of the unitary group U(N) and q fundamental representations of the orthogonal group O(N). Therefore, $U{(N)}^{\otimes r}\otimes O{(N)}^{\otimes q}$ invariants are tensor model observables endowed with a tensor field of order (r, q). We enumerate these observables using group theoretic formulae, for tensor fields of arbitrary order (r, q). Inspecting lower-order cases reveals that, at order (1, 1), the number of invariants corresponds to a number of 2- or 4-ary necklaces that exhibit pattern avoidance, offering insights into enumerative combinatorics. For a general order (r, q), the counting can be interpreted as the partition function of a topological quantum field theory (TQFT) with the symmetric group serving as gauge group. We identify the 2-complex pertaining to the enumeration of the invariants, which in turn defines the TQFT, and establish a correspondence with countings associated with covers of diverse topologies. For $r>1$, the number of invariants matches the number of (q-dependent) weighted equivalence classes of branched covers of the 2-sphere with r branched points. 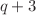At $r=1$, the counting maps to the enumeration of branched covers of the 2-sphere with $q+3$ branched points. The formalism unveils a wide array of novel integer sequences that have not been previously documented. We also provide various codes for running computational experiments.