https://doi.org/10.1140/epjc/s10052-024-13074-0
Regular Article - Theoretical Physics
Analytical calculation of Kerr and Kerr-Ads black holes in f(R) theory
1
College of Mathematics and Physics, Hunan University of Arts and Sciences, 3150 Dongting Dadao, 415000, Changde, Hunan, China
2
Hunan Province Key Laboratory Integration and Optical Manufacturing Technology, 3150 Dongting Dadao, 415000, Changde, Hunan, China
3
Division of Mathematica and Theoretical Physics, Shanghai Normal University, 100 Guilin Road, 200234, Shanghai, China
4
Center for Astrophysics, Guangzhou University, 230 West Ring Road, 510006, Guangzhou, Guangdong, China
Received:
29
April
2024
Accepted:
30
June
2024
Published online:
16
July
2024
In this paper, we extend Chandrasekhar’s method of calculating rotating black holes into f(R) theory. We show that the solution with constant Ricci scalar always exists in a general f(R) gravity and derive the Kerr and Kerr-Ads metric by using the analytical mathematical method. Suppose that the spacetime is a 4-dimensional Riemannian manifold with a general stationary axisymmetric metric, we calculate Cartan’s equation of structure and derive the Einstein tensor. In order to reduce the solving difficulty, we fix the gauge freedom to transform the metric into a more symmetric form. We solve the field equations in the two cases of the Ricci scalar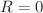 
and 
. In the case of 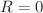, the Ernst’s equations are derived. We give the elementary solution of Ernst’s equations and show the way to obtain more solutions including Kerr metric. In the case of , we reasonably assume that the solution to the equations consists of two parts: the first is Kerr part and the second is introduced by the Ricci scalar. Giving solution to the second part and combining the two parts, we obtain the Kerr-Ads metric. The calculations are carried out in a general f(R) theory. Furthermore, the whole solving process can be treated as a standard calculation procedure to obtain rotating black holes, which can be applied to other modified gravities.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
