https://doi.org/10.1140/epjc/s10052-024-12719-4
Regular Article - Theoretical Physics
Particle dynamics in spherically symmetric electro-vacuum instantons
Université de Picardie, LAMFA (UMR 7352 du CNRS), 33 rue St Leu, 80039, Amiens Cedex 1, France
Received:
15
February
2024
Accepted:
22
March
2024
Published online:
9
April
2024
In this paper, we study the geodesic motion in spherically symmetric electro-vacuum Euclidean solutions of the Einstein equation. There are two kinds of such solutions: the Euclidean Reissner–Nordström (ERN) metrics, and the Bertotti–Robinson-like (BR) metrics, the latter having constant Kretschmann scalar. First, we derive the motion equations for the ERN spacetime and we generalize the results of Battista–Esposito, showing that all orbits in as ERN spacetime are unbounded if and only if it has an event horizon. We also obtain the Weierstrass form of the polar radial motion, providing an efficient tool for numerical computations. We then study the angular deflection of orbits in the Euclidean Schwarzschild spacetime which, in contrast to the Lorentzian background, can be either positive or negative. We observe the presence of a null and a maximal deflection rings for particles with velocity at infinity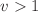 
and we give approximate values for their size when 
For BR spacetimes, we obtain analytic solutions for the radial motion in proper length, involving (hyperbolic) trigonometric functions and we deduce that orbits either exponentially go to the singularity or are periodic. Finally, we apply the previous results and use algorithms related to Weierstrass’ elliptic functions to produce a Python code to plot orbits of the spacetimes ERN and BR, and draw “shadows” of the first ones, as it was already done before for classical black holes.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
