https://doi.org/10.1140/epjc/s10052-024-12614-y
Regular Article - Theoretical Physics
Moduli space of logarithmic states in critical massive gravities
Department of Physics, University of Pretoria, Private Bag X20, 0028, Hatfield, South Africa
Received:
1
December
2023
Accepted:
25
February
2024
Published online:
12
March
2024
We take new algebraic and geometric perspectives on the combinatorial results recently obtained on the partition functions of critical massive gravities conjectured to be dual to Logarithmic CFTs through the AdS
/LCFT
correspondence. We show that the partition functions of logarithmic states can be expressed in terms of Schur polynomials. Subsequently, we show that the moduli space of the logarithmic states is the symmetric product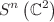 
. As the quotient of an affine space by the symmetric group, this orbifold space is shown to be described by Hilbert series that have palindromic numerators. The palindromic properties of the Hilbert series indicate that the orbifolds are Calabi-Yau, and allow for a new interpretation of the logarithmic state spaces in critical massive gravities as Calabi-Yau singular spaces.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
