Bayesian analysis of systematic errors in the determination of the constant of gravitation

Stefano Rinaldi; Hannah Middleton; Walter Del Pozzo; Jonathan Gair

doi:10.1140/epjc/s10052-023-12078-6

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2023) 83: 891
https://doi.org/10.1140/epjc/s10052-023-12078-6

Regular Article - Theoretical Physics

Bayesian analysis of systematic errors in the determination of the constant of gravitation

Stefano Rinaldi¹^,2^a, Hannah Middleton³^,4, Walter Del Pozzo¹^,2 and Jonathan Gair⁵

¹ Dipartimento di Fisica “E. Fermi”, Università di Pisa, 56127, Pisa, Italy
² INFN, Sezione di Pisa, 56127, Pisa, Italy
³ Institute for Gravitational Wave Astronomy and School of Physics and Astronomy, University of Birmingham, B15 2TT, Birmingham, UK
⁴ OzGrav-Melbourne and School of Physics, University of Melbourne, 3010, Parkville, VIC, Australia
⁵ Max Planck Institute for Gravitational Physics (Albert Einstein Institute), Am Mühlenberg 1, 14476, Potsdam, Germany

^a stefano.rinaldi@phd.unipi.it

Received: 29 August 2023
Accepted: 23 September 2023
Published online: 4 October 2023

Abstract

Measurements of the gravitational constant G are notoriously difficult. Individual state-of-the-art experiments have managed to determine the value of G with high precision: although, when considered collectively, the range in the measured values of G far exceeds individual uncertainties, suggesting the presence of unaccounted for systematic effects. Here, we propose a Bayesian framework to account for the presence of systematic errors in the various measurement of G while proposing a consensus value, following two paths: a parametric approach, based on the maximum entropy principle, and a non-parametric one, the latter being a very flexible approach not committed to any specific functional form. With both our methods, we find that the uncertainty on this fundamental constant, once systematics are included, is significantly larger than what quoted in CODATA 2018. Moreover, the morphology of the non-parametric distribution hints towards the presence of several sources of unaccounted for systematics. In light of this, we recommend a consensus value for the gravitational constant 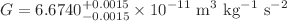$G = 6 . 6740_{- 0.0015}^{+ 0.0015} \times 10^{- 11} m^{3} {kg}^{- 1} s^{- 2}$ $G = 6.6740^{+0.0015}_{-0.0015} \times 10^{-11}\ \textrm{m}^3\ \textrm{kg}^{-1}\ \textrm{s}^{-2}$ .

© The Author(s) 2023

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.