Analysis of the strong vertices of and in QCD sum rules

Jie Lu; Guo-Liang Yu; Zhi-Gang Wang; Bin Wu

doi:10.1140/epjc/s10052-023-12076-8

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2023) 83: 907
https://doi.org/10.1140/epjc/s10052-023-12076-8

Regular Article - Theoretical Physics

Analysis of the strong vertices of $Σ_{c} Δ D^{}$ $\Sigma _{c}\Delta D^{}$ and $Σ_{b} Δ B^{}$ $\Sigma _{b}\Delta B^{}$ in QCD sum rules

Jie Lu¹^,2, Guo-Liang Yu¹^,2^b, Zhi-Gang Wang¹ and Bin Wu¹

¹ Department of Mathematics and Physics, North China Electric Power University, 071003, Baoding, People’s Republic of China
² Hebei Key Laboratory of Physics and Energy Technology, North China Electric Power University, 071000, Baoding, China

^b yuguoliang2011@163.com

Received: 13 August 2023
Accepted: 24 September 2023
Published online: 9 October 2023

Abstract

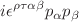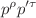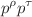In this work, we analyze the strong vertices $Σ_{c} Δ D^{*}$ $\Sigma _{c}\Delta D^{*}$ and $Σ_{b} Δ B^{*}$ $\Sigma _{b}\Delta B^{*}$ using the three-point QCD sum rules under the tensor structures $i ϵ^{ρ τ α β} p_{α} p_{β}$ $i\epsilon ^{\rho \tau \alpha \beta }p_{\alpha }p_{\beta }$ , $p^{ρ} p^{' τ}$ $p^{\rho }p'^{\tau }$ and $p^{ρ} p^{τ}$ $p^{\rho }p^{\tau }$ . 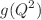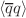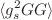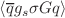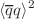We firstly calculate the momentum dependent strong coupling constants $g (Q^{2})$ $g(Q^{2})$ by considering contributions of the perturbative part and the condensate terms $⟨ \bar{q} q ⟩$ $\langle {\overline{q}}q\rangle$ , $⟨ g_{s}^{2} G G ⟩$ $\langle g_{s}^{2}GG \rangle$ , $⟨ \bar{q} g_{s} σ G q ⟩$ $\langle {\overline{q}}g_{s}\sigma Gq\rangle$ and ${⟨ \bar{q} q ⟩}^{2}$ $\langle {\overline{q}}q\rangle ^{2}$ . By fitting these coupling constants into analytical functions and extrapolating them into time-like regions, we then obtain the on-shell values of strong coupling constants for these vertices. The results are $g_{1 Σ_{c} Δ D^{*}} = 5 . 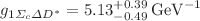13_{- 0.49}^{+ 0.39} {GeV}^{- 1}$ $g_{1\Sigma _{c}\Delta D^{*}}=5.13^{+0.39}_{-0.49}\,\hbox {GeV}^{-1}$ , $g_{2 Σ_{c} Δ D^{*}} = - 3 . 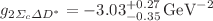03_{- 0.35}^{+ 0.27} {GeV}^{- 2}$ $g_{2\Sigma _{c}\Delta D^{*}}=-3.03^{+0.27}_{-0.35}\,\hbox {GeV}^{-2}$ , $g_{3 Σ_{c} Δ D^{*}} = 17 . 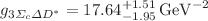64_{- 1.95}^{+ 1.51} {GeV}^{- 2}$ $g_{3\Sigma _{c}\Delta D^{*}}=17.64^{+1.51}_{-1.95}\,\hbox {GeV}^{-2}$ , $g_{1 Σ_{b} Δ B^{*}} = 20 . 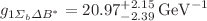97_{- 2.39}^{+ 2.15} {GeV}^{- 1}$ $g_{1\Sigma _{b}\Delta B^{*}}=20.97^{+2.15}_{-2.39}\,\hbox {GeV}^{-1}$ , $g_{2 Σ_{b} Δ B^{*}} = - 11 . 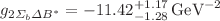42_{- 1.28}^{+ 1.17} {GeV}^{- 2}$ $g_{2\Sigma _{b}\Delta B^{*}}=-11.42^{+1.17}_{-1.28}\,\hbox {GeV}^{-2}$ and $g_{3 Σ_{b} Δ B^{*}} = 24 . 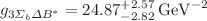87_{- 2.82}^{+ 2.57} {GeV}^{- 2}$ $g_{3\Sigma _{b}\Delta B^{*}}=24.87^{+2.57}_{-2.82}\,\hbox {GeV}^{-2}$ . These strong coupling constants are important parameters which can help us to understand the strong decay behaviors of hadrons.

© The Author(s) 2023

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.