https://doi.org/10.1140/epjc/s10052-023-11236-0
Regular Article - Theoretical Physics
Approximate N
LO parton distribution functions with theoretical uncertainties: MSHT20aN
LO PDFs
1
Department of Physics and Astronomy, University College London, WC1E 6BT, London, UK
2
Rudolf Peierls Centre, Beecroft Building, Parks Road, OX1 3PU, Oxford, UK
Received:
8
August
2022
Accepted:
19
January
2023
Published online:
1
March
2023
We present the first global analysis of parton distribution functions (PDFs) at approximate NLO in the strong coupling constant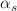 
, extending beyond the current highest NNLO achieved in PDF fits. To achieve this, we present a general formalism for the inclusion of theoretical uncertainties associated with the perturbative expansion in the strong coupling. We demonstrate how using the currently available knowledge surrounding the next highest order (NLO) in 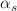can provide consistent, justifiable and explainable approximate NLO (aNLO) PDFs. This includes estimates for uncertainties due the currently unknown NLO ingredients, but also implicitly some missing higher order uncertainties (MHOUs) beyond these. Specifically, we approximate the splitting functions, transition matrix elements, coefficient functions and K-factors for multiple processes to NLO. Crucially, these are constrained to be consistent with the wide range of already available information about NLO to match the complete result at this order as accurately as possible. Using this approach we perform a fully consistent approximate NLO global fit within the MSHT framework. This relies on an expansion of the Hessian procedure used in previous MSHT fits to allow for sources of theoretical uncertainties. These are included as nuisance parameters in a global fit, controlled by knowledge and intuition based prior distributions. We analyse the differences between our aNLO PDFs and the standard NNLO PDF set, and study the impact of using aNLO PDFs on the LHC production of a Higgs boson at this order. Finally, we provide guidelines on how these PDFs should be used in phenomenological investigations.
The original online version of this article was revised: The changes are contained within Table 2, Table 8 and also on page 45 and 54.
An erratum to this article is available online at https://doi.org/10.1140/epjc/s10052-023-11451-9.
Copyright comment corrected publication 2023
© The Author(s) 2023. corrected publication 2023
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
