https://doi.org/10.1140/epjc/s10052-022-10649-7
Regular Article - Theoretical Physics
Scattering of fermionic isodoublets on the sine-Gordon kink
Tomsk State University of Control Systems and Radioelectronics, 634050, Tomsk, Russia
Received:
17
May
2022
Accepted:
27
July
2022
Published online:
2
August
2022
The scattering of Dirac fermions on the sine-Gordon kink is studied both analytically and numerically. To achieve invariance with respect to a discrete symmetry, the sine-Gordon model is treated as a nonlinear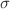 
-model with a circular target space that interacts with fermionic isodublets through the Yukawa interaction. It is shown that the diagonal and antidiagonal parts of the fermionic wave function interact independently with the external field of the sine-Gordon kink. The wave functions of the fermionic scattering states are expressed in terms of the Heun functions. General expressions for the transmission and reflection coefficients are derived, and their dependences on the fermion momentum and mass are studied numerically. The existence condition is found for two fermionic zero modes, and their analytical expressions are obtained. It is shown that the zero modes do not lead to fragmentation of the fermionic charge, but can lead to polarization of the fermionic vacuum. The scattering of the diagonal and antidiagonal fermionic states is found to be significantly different; this difference is shown to be due to the different dependences of the energy levels of these bound states on the fermion mass, and is in accordance with Levinson’s theorem.
© The Author(s) 2022
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
