https://doi.org/10.1140/epjc/s10052-022-10135-0
Regular Article - Theoretical Physics
A study of cylindrically symmetric solutions in 
theory of gravity
1
Department of Mathematics, University of Management and Technology, Sialkot Campus, Lahore, Pakistan
2
Department of Mathematics, College of Science, King Khalid University, 9004, Abha, Saudi Arabia
Received:
18
October
2021
Accepted:
10
February
2022
Published online:
22
February
2022
In this article, we aim to investigate some cylindrically symmetric solutions in a very well known modified theory named as theory of gravity, where the terms R,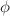 
and X are clarified as Ricci Scalar, scalar potential, and kinetic term respectively. For this purpose, we consider the cylindrically symmetric space-time to discuss the cylindrical solutions in some realistic regions. We further discuss six distinct cases of exact solutions using the field equations of modified theory of gravity. Furthermore, we set some suitable values of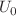 
and 
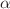in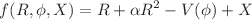 
for the investigation of well-known Levi–Civita and cosmic string solutions. The Energy conditions are also investigated for all different cases and observed that null energy conditions are violated, which is the indication of the existence of cylindrical wormholes.
© The Author(s) 2022
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
